Digital Evolution as a Teaching Tool

A while back I designed this small project with two 9th grade students during their week-long internship in my lab. The goal was to introduce evolutionary algorithms in an accessible, visual way.

I chose colors as our system — something intuitive yet powerful for demonstrating computational evolution. Each individual in our population is represented by a color, with its genome being the RGB color code. Its fitness is calculated as the negative Euclidean distance between its RGB values and those of a target color. Generation after generation, the most fit individuals reproduce more frequently, gradually shifting the population toward the objective. Parents are selected from the highest performers and reproduce asexually, with random mutations applied to their color codes.

What makes this project compelling is how it transforms abstract computational concepts into immediate visual feedback. The evolutionary process becomes both a learning tool and a generator of striking visual patterns.

Visualizing the Evolutionary Process

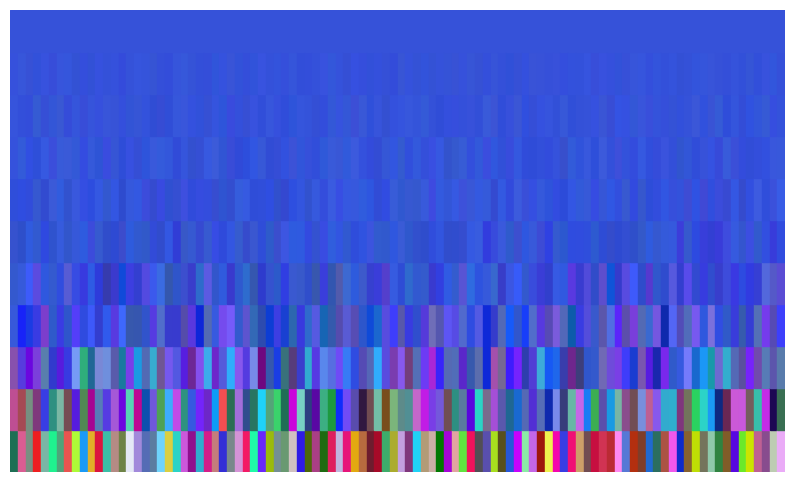
In our visualization system, each patch represents an individual and its color, while each horizontal line represents a generation. Time moves upward, with the target color displayed in the top line.

The example above shows a successful evolutionary run. The initial randomness of the population gradually gives way to convergence as selection pressure and reproduction drive the colors toward the target.

Parameter Space and Visual Diversity

The interplay between parameter settings and visual outcomes becomes evident when we experiment with population size. Below, a smaller population reduces initial diversity and makes exploring the color space more difficult. The evolutionary process converges prematurely, missing the target color.

To address this limitation, we can increase mutation strength, allowing children to differ more significantly from their parents. This intervention reintroduces diversity and improves exploration. Notice the greater variation across individuals in the latest generations – this increased diversity helps solve the convergence problem.

With larger populations (around 100 individuals), the inherent diversity allows for smaller mutation rates. This combination leads to finer convergence with less variation in the final generations, achieving nearly perfect alignment with the target color.

Evolution Gallery

Each of these evolutionary runs represents a different parameter configuration and starting condition. The resulting visual patterns reveal the underlying computational dynamics – how selection pressure, mutation rates, and population size interact to create different evolutionary trajectories.